Simplifying Trigonometry Using Euler's Formula

The Most Remarkable Formula in Mathematics

The Pythagorean theorem, which expresses the relationship between the lengths of sides of a right-angled triangle, stands as a symbol of the mathematical prowess of the ancient Greeks. This elegant theorem captivated minds throughout history, drawing the attention of renowned figures like Albert Einstein and former US President James Garfield. Both Einstein and Garfield presented novel proofs to this fundamental result. Furthermore, the Pythagorean theorem played a pivotal role in shaping modern mathematics. Its applications extend beyond Euclidean geometry, influencing fields such as Cartesian geometry and calculus.

When future scholars examine the accomplishments of modern mathematicians since the 16th century, they will see a remarkable formula derived by Swiss mathematician Leonhard Euler in the same light. Theoretical physicist Richard Feynman called it "the most remarkable formula in mathematics" and "our jewel" in his Lectures on Physics. Euler’s formula connects many apparently distinct branches of mathematics, such as geometry, logarithm and complex numbers. Its applications are found ubiquitously in quantum mechanics, signal processing, electrical engineering and number theory.

Euler’s Formula

Despite its formidable presence in many branches of mathematics and physics, Euler's formula is rather simple. It is written as -

\(\begin{equation} e^{i\theta} =\cos{(\theta)}+i \sin{(\theta)} \end{equation}\)

Let us plug a few values for theta to see what the equation produces.

For theta=0,

\(\begin{equation} e^{i0} = \cos 0 + i\sin 0 = 1 \end{equation}\)

There is no surprise here, because 0-th power of any number is 1. We can use the above result to remember that $\cos 0$ is 1 and $\sin 0$ is 0.

For theta=pi/2,

\(\begin{equation} e^{i\pi/2} = \cos\pi/2 + i\sin\pi/2 = i \end{equation}\)

The above result is often used to express “i” as an exponential.

For theta=pi,

\(\begin{equation} e^{i \pi} = \cos\pi + i\sin\pi = -1 \end{equation}\)

The above result is quite remarkable, because it ties together fundamental constants “e”, “pi” and “i” originating from distant branches of mathematics.

Widespread Applications

The real power of Euler's formula is in its applications. Learning to use it has immense practical value, because it saves one from memorizing hundreds of trigonometric relations. I remember that memorizing those rules to be the biggest obstacle of high-school trigonometry. Our exams did not provide formula sheets, and therefore we had to keep all these relations off the top of our heads. We had to know the rules for sines and cosines of special angles, the rules for sums, differences and multiples of angles, and, with calculus, also the rules for derivatives of sines and cosines.

Some time late in high-school, I got introduced to Euler's formula, and it brought down my list of equations to a single one. Euler's formula not only allowed me to derive most trigonometric equations on the fly, but also helped me solve complex integrations like the one shown below. I request you to try it using traditional methods (integration by parts) to fully appreciate the power of the Euler's formula.

\(\int e^{ax} \cos(bx) dx\)

Application 1 - Deriving sin(4A)

Usually trigonometry students are asked to memorize the expansions of sin(2A) and sin(3A) and the corresponding cosine rules. With Euler's formula, all those results can be derived in seconds. We will go one step further and derive the expansion of sin(4A) to illustrate the power of Euler's formula.

Here is the game plan. We will expand e to the power (i4A) in two different ways and then compare the real and imaginary parts of both expansions.

Expanding in the first way -

\(\begin{equation} e^{i4A} =\cos{(4A)}+i \sin{(4A)} \end{equation}\)

Expanding in the second way -

\(\begin{equation} e^{i4A} =(e^{iA})^4 =(\cos{A}+i \sin{A})^4 \end{equation}\)

Application of binomial expansion gives us -

\(\begin{equation} e^{i4A} = \cos^4{A} + 4i \cos^3{A} \sin{A} -6 \cos^2{A} \sin^2{A} \\ - 4i \cos{A} \sin^3{A} + \sin^4{A} \end{equation}\)

Now that we have e to the power 4iA derived in two ways, we can separately compare the real and imaginary parts of both expansions. We get -

\(\begin{equation} \boxed{ \cos{(4A)} = \cos^4 A + \sin^4 A -6 \cos^2 A \sin^2 A \\ } \end{equation}\)

\(\begin{equation} \boxed{ \sin{(4A)} = 4 \cos^3 A \sin A - 4 \cos A \sin^3 A } \end{equation}\)

Irrespective of whether you like to compute sin(2A), sin(3A) or even sin(10A), you can use the above method to get the results with minimal effort. Always you will get the the rule for the corresponding cos function with no extra effort.

Application 2 - Finding the Square Root of i

\(i = e^{i\pi/2}\)

\(\sqrt{i} = e^{i\pi/4} = \cos(\pi/4) + i \sin(\pi/4) = \frac{1}{\sqrt{2}} + \frac{i}{\sqrt{2}}\)

But is that the only result? To understand, we need to first take a look at the geometric interpretation of Euler’s formula.

Geometric Interpretation

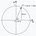
https://upload.wikimedia.org/wikipedia/commons/7/71/Euler%27s_formula.svg

Before giving complete answers to Applications 2 and 3 above, we need to learn how to interpret the result geometrically. In the above figure (from here), the coordinate axes represent the real and imaginary parts of complex numbers. The number e to the power “i theta” is always on the unit circle (center = 0, radius = 1), and the line connecting it with the origin has an angle theta with the real axis. Therefore, the real and imaginary parts have the values cos(theta) and sin(theta) respectively. We can easily verify the above claims using a few specific values of theta such as 0, pi/4, pi/2, pi and 2*pi.

Please note that the values of the angles in trigonometry are not restricted to (0, 2*pi). We can keep going around the circle multiple times, and generate any positive or negative angle. Every anti-clockwise trip around the circle increases theta by 2*pi but brings us back to the same point on the graph. Therefore,

\(\begin{equation} 1= e^{i0} = e^{2i\pi} = e^{4i\pi} = e^{6i\pi} \end{equation}\)

and so on.

Similarly, on the negative side,

\(\begin{equation} 1 = e^{-2i\pi} = e^{-4i\pi} = e^{-6i\pi} \end{equation}\)

and so on. You can arbitrarily increase the angle in Euler's formula by multiples of 2*pi and still get the same complex number.

With this insight, let us revisit the questions of square root of “i” and 1 to the power “i”. We can write .

\(\begin{equation} 1^i = e^{i^20} = e^{2i^2\pi} = e^{4i^2\pi} = e^{6i^2\pi} = e^{-2i^2\pi} = e^{-4i^2\pi} = $e^{-6i^2\pi} \end{equation}\)

Simplifying these results,

\(\begin{equation} 1^i = e^{-2n\pi} \end{equation}\)

where n is any integer. The value of 1 derived previously is for n = 0.

This is not completely unexpected. We get multiple values for fractional powers of 1. For example, square root (or power = 1/2) of 1 has values +1 and -1, and cube root (or power=1/3) of 1 gives us three solutions. Therefore, it is not a stretch to accept that imaginary powers of 1 have infinite values.

Readers can work out similar logic to derive two values for square root of “i” -

\(\begin{equation} \sqrt{i} = \frac{1\pm i}{2} \end{equation}\)

The derivation is explained in detail in my tutorial along with several other interesting applications of Euler's formula.

A Source of Immense Beauty

Ever since I learned about Euler's formula, I always marveled at its power in revealing the intrinsic symmetry within trigonometric rules. I was never satisfied with the arbitrariness of many rules in trigonometry. For example, why does cos(A+B) have minus in its expansion, whereas the expansion of sin(A+B) has a plus sign? Similarly, why does the triangle identity for cos(A/2) cos(B/2) cos(C/2) have an extra 1 added to the sum, but sin(A/2) sin(B/2) sin(C/2) does not? Euler's formula explains these apparent asymmetries, and it is covered in my tutorial.

The second benefit of Euler's equation is that you always get "buy one, get one free" deals !! Two equations can be derived with less effort than one with traditional methods. You can see that in the derivation of sin(4A) above, where we also derived the expansion of cos(4A) as a side product. I present many more examples in the tutorial.